Magic Squares
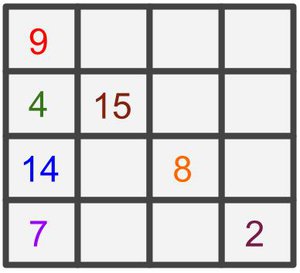
Suppose we have a 4 x 4 magic square as shown in the diagram. The sum of each row, column and diagonal must be the same. Additionally, each number (1 to 16) may only be used once.
This type of problem can easily be solved using Google OR-Tools CP-SAT Solver.
Here is how to do it using Python:
Declare the CP-SAT model:
model = cp_model.CpModel()
Create the decision variables:
# 0 1 2 3
# 4 5 6 7
# 8 9 10 11
# 12 13 14 15
numbers = [model.NewIntVar(1, 16, f"h{str(i)}") for i in range(1, 17)]
Add a constraint that all the decision variables be different:
model.AddAllDifferent(numbers)
Add constraints for all rows, columns and diagonals to sum to 34:
model.Add(sum(number for position, number in enumerate(numbers) if position in (0, 1, 2, 3)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (4, 5, 6, 7)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (8, 9, 10, 11)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (12, 13, 14, 15)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (0, 4, 8, 12)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (1, 5, 9, 13)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (2, 6, 10, 14)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (3, 7, 11, 15)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (0, 5, 10, 15)) == 34) model.Add(sum(number for position, number in enumerate(numbers) if position in (3, 6, 9, 12)) == 34)
Add a constraint to set the decision variables as per the diagram:
model.Add(numbers[0] == 9) model.Add(numbers[4] == 4) model.Add(numbers[5] == 15) model.Add(numbers[8] == 14) model.Add(numbers[12] == 7) model.Add(numbers[10] == 8) model.Add(numbers[15] == 2)
Call the CP-SAT solver:
solver = cp_model.CpSolver() solver.Solve(model)
Configure a solution printer (so all solutions are printed nicely):
solution_printer = VarArraySolutionPrinter(numbers)
Search for all possible solutions:
status = solver.SearchForAllSolutions(model, solution_printer)
Print the status of the solutions (OPTIMAL, FEASIBLE, INFEASIBLE, MODEL_INVALID or UNKNOWN):
print(f"Status = {solver.StatusName(status)}")
Print the number of solutions found:
print(f"Number of solutions found: {solution_printer.solution_count()}")
Here is the code output:
9 6 3 16 4 15 10 5 14 1 8 11 7 12 13 2 Status = OPTIMAL Number of solutions found: 1
The only bits I left out go at the top of the Python script.
These are importing the CP-SAT model and configuring the solution printer by overriding the methods appropriately.
See these in the full listing of the code below:
from ortools.sat.python import cp_model
class VarArraySolutionPrinter(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, variables):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__variables = variables
self.__solution_count = 0
def on_solution_callback(self):
self.__solution_count += 1
# for v in self.__variables:
# print('%s=%i' % (v, self.Value(v)), end=' ')
vars = list(self.__variables)
print(
f"{self.Value(vars[0])} "
f"{self.Value(vars[1])} "
f"{self.Value(vars[2])} "
f"{self.Value(vars[3])}"
)
print(
f"{self.Value(vars[4])} "
f"{self.Value(vars[5])} "
f"{self.Value(vars[6])} "
f"{self.Value(vars[7])}"
)
print(
f"{self.Value(vars[8])} "
f"{self.Value(vars[9])} "
f"{self.Value(vars[10])} "
f"{self.Value(vars[11])} "
)
print(
f"{self.Value(vars[12])} "
f"{self.Value(vars[13])} "
f"{self.Value(vars[14])} "
f"{self.Value(vars[15])} "
)
print()
def solution_count(self):
return self.__solution_count
model = cp_model.CpModel()
# 0 1 2 3
# 4 5 6 7
# 8 9 10 11
# 12 13 14 15
numbers = [model.NewIntVar(1, 16, f"h{str(i)}") for i in range(1, 17)]
model.AddAllDifferent(numbers)
model.Add(sum(number for position, number in enumerate(numbers) if position in (0, 1, 2, 3)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (4, 5, 6, 7)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (8, 9, 10, 11)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (12, 13, 14, 15)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (0, 4, 8, 12)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (1, 5, 9, 13)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (2, 6, 10, 14)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (3, 7, 11, 15)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (0, 5, 10, 15)) == 34)
model.Add(sum(number for position, number in enumerate(numbers) if position in (3, 6, 9, 12)) == 34)
model.Add(numbers[0] == 9)
model.Add(numbers[4] == 4)
model.Add(numbers[5] == 15)
model.Add(numbers[8] == 14)
model.Add(numbers[12] == 7)
model.Add(numbers[10] == 8)
model.Add(numbers[15] == 2)
solver = cp_model.CpSolver()
solver.Solve(model)
solution_printer = VarArraySolutionPrinter(numbers)
status = solver.SearchForAllSolutions(model, solution_printer)
print(f"Status = {solver.StatusName(status)}")
print(f"Number of solutions found: {solution_printer.solution_count()}")